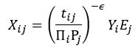Industry News // Statistics Canada releases methodology for estimating changes to North American trade patterns
Study: Estimating the effect of changing Canada/United States border costs on North American trade patterns and expenditures – detailed methodology
Statistics Canada recently completed a report on the methods used for estimating the effect of changing Canada-US border costs on North American trade. This paper is a follow-up to a previous report that provided detailed results of the study. The paper discusses in greater detail how Statistics Canada used its Surface Transportation File (STF), United States (US) domestic trade data, and a gravity trade model framework to study trade flows among 201 Canadian and United States regions for 2012. The paper also highlights a number of desirable properties of the Poisson Pseudo Maximum Likelihood (PPML) estimator, such as robustness to heteroscedasticity, the ability to hand zero-valued trade flows, and how the estimator simplifies the estimation of general equilibrium effects by satisfying adding-up constraints.
A large body of research has estimated average bilateral border costs, the combined effect of tariff and non-tariff barriers, indirectly by applying the gravity trade model framework, with border costs usually expressed as a tariff rate equivalent. Recent economic studies using this approach suggest further research is needed to accurately estimate these border costs, with concerns raised over the limited information on trade flows found in studied datasets. Geographic aggregation, to national levels or sub-national levels like provinces or states, has been found to introduce upward bias in the estimated border costs. This issue was addressed by another recent Statistics Canada study (Bemrose, Brown and Tweedle 2017), which used highly detailed trade data from the Surface Transportation File (STF).
The Gravity Model
Gravity models of trade originated with the preposition that bilateral trade flows should be increasing with the economic sizes of trading partners, and decreasing in their distance. The seminal work of Anderson and van Wincoop (2003) provided the first of many theoretical justifications for the gravity model, which showed that in addition to size and proximity, gravity models should also incorporate “multilateral resistance” terms to capture the influence of other trading partners. The gravity model for exports from location i to j (Xij) can be written as:
where Πi and Pj are the multilateral resistance terms, Yi is total output for location i, Ej is location j’s total expenditures on goods and services from all locations, tij is the bilateral trade cost, and −ε is the trade cost elasticity.
Data
The STF was built from shipping records to measure domestic trade between detailed locations within Canada and between the United States and Canada. This dataset was combined with US Commodity Flow Survey (CFS) data to produce trade flow data among 201 comparable Canadian and United States regions for 2012. The resulting dataset is one of the most geographically detailed trade datasets available for measuring the average cost of the Canada-US and provincial borders.
Finer geographic detail should provide better estimates of average shipping distances between economic regions, and make intraregional trade costs more homogeneous across geographical units. Previous studies have suggested that measurement errors in distance and large differences in intraregional trade costs can cause substantial bias in estimated border costs. Sub-State and Sub-Provincial geographies were created for this study using the CFS’s division of states into metropolitan and non-metropolitan (MA/non-MA) areas, and the aggregation of STF trade flows into Economic Regions (ERs) comparable in size to the US MA/non-MA geography.
Most research is limited to using great circle distances between arbitrary points within trading areas. These measures often mischaracterize the distance goods traded between regions actually travel. The STF and CFS allow the derivation of network distances that more accurately reflect the origins, destinations and journeys goods can be expected to take.
Estimation
The gravity model has traditionally been estimated by taking the natural log and using ordinary least squares (OLS). However, Silva and Tenreyro (2006) show that this approach leads to biased estimates in the presence of heteroskedasticity due to the retransformation problem. The authors suggest estimating the gravity equation in multiplicative form using Poisson Pseudo Maximum Likelihood (PPML) estimation. PPML is robust to heteroscedasticity and has the added benefit of being able to accommodate zero-valued observations for the dependant variable (i.e. zero-valued trade flows). Fally (2015) shows that importer and exporter fixed effects estimated by PPML will always satisfy the adding-up conditions for the multilateral resistance terms, simplifying the process of estimating full general equilibrium effects of changes to border costs.
For the econometric specification, the functional form of the multilateral resistance terms need not be identified to estimate the gravity model, since these terms can be replaced with importer and exporter fixed effects. Proxy variables are used to capture bilateral trade costs, which include distance and dummy variables that indicate if a provincial border, state border, or the Canadian-US border separates the two regions. In much of the literature, the trade cost of exporting from region i to region j is assumed to be a log-linear function of distance. This assumption is likely problematic when using a fine geographic breakdown, as trade involves both fixed and variable transportation costs. To account for possible nonlinearities in the effect of distance, a spline function is defined over various ranges of distance.
Results
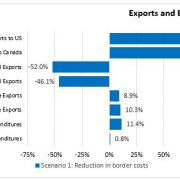
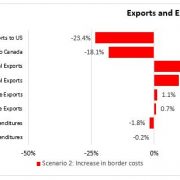
The results suggest that the tariff rate equivalent for the Canada-US border is in the neighborhood of 30%, while the provincial border imposes a cost equivalent to a 10% tariff, on average. To gauge the significance of these costs, model estimates are used to evaluate the general equilibrium effects of changing Canada-US border costs through two counter factual scenarios. First, the cost of trading between Canada and the United States is assumed to be equivalent to trading across provincial borders. This amounts to reducing the Canada-US border cost to a 10% tariff equivalent. The second scenario is representative of Canada and the US withdrawling from a preferential trading agreement (i.e. NAFTA). For this case, it is assumed that the Canada-US border cost would increase to a 36% tariff equivalent.
Results suggest that reducing the cost of the Canada-US border from 30 to 10 per cent will lead to an 82.2 per cent increase in exports from Canada to the United States, a 52.0 per cent decrease in inter-provincial exports, and a 46.1 per cent decline in intra-provincial exports. In addition, expenditure on domestic and imported non-energy goods increases 11.4% in Canada.
Estimates also suggest that increasing the Canada-US border cost from 30 to 36 per cent would reduce Canadian exports to the United States by 23.4 per cent and increase trade within Canada with inter-provincial exports rising 11.3 per cent and intra-provincial trade increasing 9.8 per cent. The authors also find that the higher border cost would reduced non-energy goods expenditures by 1.8 per cent (approximately $10 billion CAD in 2012).
References
Anderson, J. E. and E. van Wincoop (2003). Gravity with Gravitas: A Solution to the Border Puzzle. American Economic Review 93(1), 170–192.
Bemrose, R. K., W. M. Brown, and J. Tweedle (2017). Going the Distance: Estimating the Effect of Provincial Borders on Trade when Geography Matters. Analytical Studies Branch Research Paper Series, no. 394. Statistics Canada Catalogue no. 11F0019M. Ottawa: Statistics Canada.
Fally, T. (2015). Structural gravity and fixed effects. Journal of International Economics 97(1), 76–85.
Silva, J. M. C. S. and S. Tenreyro (2006). The Log of Gravity. The Review of Economics and Statistics 88(4), 641–658.